예측 모형의 성능
데이터 분석에서 궁극적인 목표는 예측 오차가 가장 작은 최적의 예측모형을 구하는 것이다. 최적의 모형을 구하기 위해서 예측모형 함수의 계수(coefficient)를 바꾸어 본다. 이때, 예측모형 함수의 계수를 모수라고 한다.
모수를 어떤 숫자로 정하느냐에 따라 예측모형의 성능(performance)이 달라진다. 따라서 모수를 결정하여 성능의 크기를 출력하는 함수를 성능함수(performance function)이라고 하며, 성능함수의 값은 클수록 좋다.
반대로 모수를 입력받아 오차 혹은 오류의 크기를 출력하는 함수를 가장 작게 하는 것을 목표로 할 수 도 있다. 이러한 함수는 손실함수(loss function), 비용함수(cost function), 또는 오차함수(error function)라 고 부른다.
성능함수, 손실함수, 비용함수, 오차함수 등 최적화의 대상이 되는 함수를 통틀어 목적함수(objective function)라고 한다.
목적함수가 주어졌을 때 이 목적함수의 값을 가장 크게 혹은 적게 할 수 있는 입력값, 즉 모수를 구하기를 원한다. 이때 이를 최적화(optmization)라고 한다. 최적화를 하기 위해서는 입력값이 변했을 때 함수의 출력값이 어떻게 달라지는지를 정량적으로 알아야 한다. 이러한 과정이 미분(differentiation)이다.
기울기
두 x 변수의 변화에 따라 y의 값 또한 변하는데, 이때 이 두 변화율 간 비율을 기울기(slope) 또는 민감도(sensitivity)라 한다.
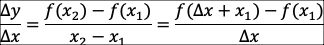
이 기울기를 평균 변화율이라고도 한다.
scipy.misc패키지의 derivative() 명령을 사용하면 수치적으로 대략적인 기울기를 계산할 수 있다.
def f(x):
return x**3 - 5*x**2 +x
from scipy.misc import derivative
print(derivative(f, 0, dx=1e-6))
print(derivative(f, 1, dx=1e-6))
>>> 1.000000000001
-5.999999999950489
미분(Differentiation)
어떤 함수의 정의역의 각각의 점에서 함숫값의 변화량과 독립변수값의 변화량 비의 극한들로 치역이 구성되는 새로운 함수다. 어떤 함수의 미분 계수 또는 순간 변화율을 구하는 것을 의미하며 미분 계수는 독립 변수 x의 증분에 관한 함숫값 ƒ(x)의 증분의 비가 한없이 일정한 값에 가까워질 때 그 일정한 값, 즉 함수에서 변수 x값의 변화량에 관한 함숫값 ƒ(x)의 변화량 비가 한없이 일정한 값에 가까워질 때 그 일정한 값 dy/dx로 나타낸다.
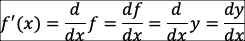
곱셈법칙
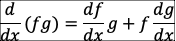
연쇄법칙

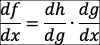
편미분
만약 함수가 둘 이상의 독립변수를 가지는 다변수 함수인 경우에도 미분할 수 있다. 이를 편미분(partial differentiation)이라고 한다. 하나의 변수에 대해서만 구할 수 있기 때문에 편미분의 결과로 하나의 함수에 대해 여러 개의 도함수가 나올 수 있다.
편미분의 결과 즉 도함수는 독립 변수를 함수의 아랫첨자로 써서 표기하거나 ∂(round) 기호를 사용하여 표기 한다. 두 개의 독립 변수를 가지는 함수 의 편미분 도함수는 다음과 같이 표기한다.

테일러 정리(Taylor's theorem)
어느 구간에서 미분가능한 함수를 유한 테일러 다항식과 근접할수록 에 가까워지는 오차항(truncation error)의 합으로 표현할 수 있다는 정리.(수학적 정의) 함수의 기울기(1차 미분값)를 알고 있다면 함수의 모양을 다음처럼 근사화할 수 있다.

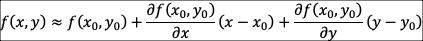
적분(integral)은 미분과 반대되는 개념이다. 적분에는 부정적분(indefinite integral)과 정적분(definite integral)이 있다.
부정적분(indefinite integral)
미분의 역연산이다. 함수가 어떤 함수를 미분하여 나온 결과인 도함수라고 가정하고 이 도함수 에 대한 미분되기 전의 원래
의 함수를 찾는 과정(integration)이다.
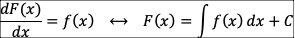
편미분의 부정적분


import sympy
sympy.init_printing(use_latex='mathjax')
x=sympy.symbol('x')
f = x * sympy.exp(x) + sympy.exp(x)
f
>>> xe^x + e^x
정적분(definite integral)
독립변수 x가 어떤 구간 [a,b] 사이일 때 그 구간에서 함수 의 값과 수평선(x 축)이 이루는 면적의 값(integral)이다. 수학 기호로는 다음과 같이 표기 한다.
